グラフィカルモデルとの出会い
ぼくの研究内容の「周辺環境を考慮する」方法として, グラフィカルモデルを利用した論文が多くあり, 精度が相当高くて衝撃を受けた！なので, 「よし！これを応用して人物行動予測につなげるぞ！」っと思ったけど, 論文に書かれている数式やアルゴリズムが全くわからない...
とりあえず, ノートに数式を書きなぐったけど, 正直ピンとこない... 特に "CRF(Conditional Random Field) : 条件付き確率場" に関しては, ググってもわからない... そんなこんなで, 1年かけてようやく理解できたぼくなりのグラフィカルモデルを簡単にまとめます.
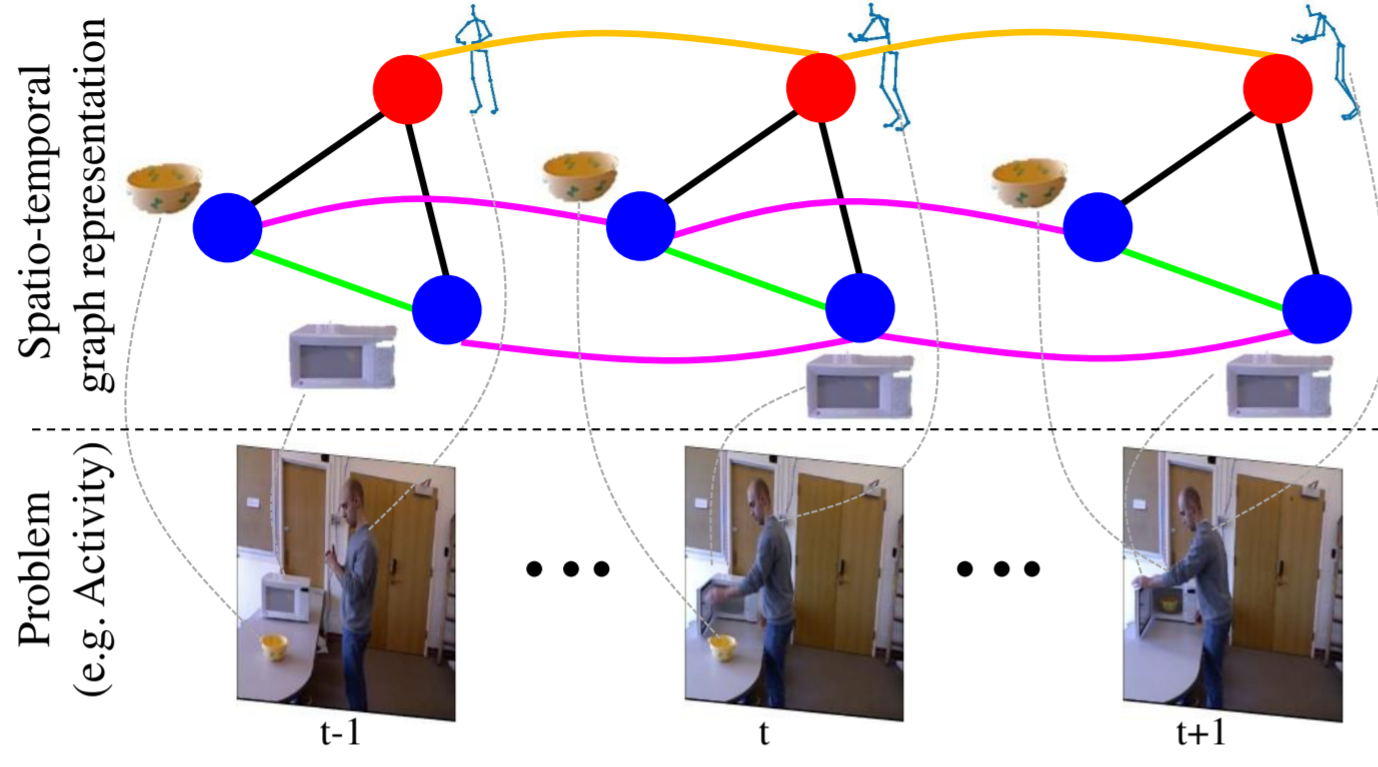Spatio-Temporal Graphを応用したい！
グラフィカルモデル
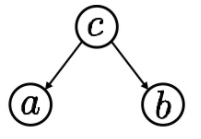
グラフィカルモデルとは , 確率変数の関係をグラフで表現したモデルである. 例えば , 3つの確率変数$a, b, c$の間に
\begin{eqnarray}
p(a,b,c) = p(a|c)p(b|c)p(c)
\end{eqnarray}
のような関係が存在する場合, この関係性は図1のように表現できる. このようにグラフ構造を用いることで, 確率モデルの構造を把握しやすくなる.
図1. グラフの例
グラフィカルモデルには, ベイジアンネットワーク(有向)とマルコフ確率場(無向)の大きく分けて2種類があり, 前者は確率的な因果関係をモデル化し, 後者では確率的な依存関係をモデル化である.
1. ベイジアンネットワーク(有向グラフ)
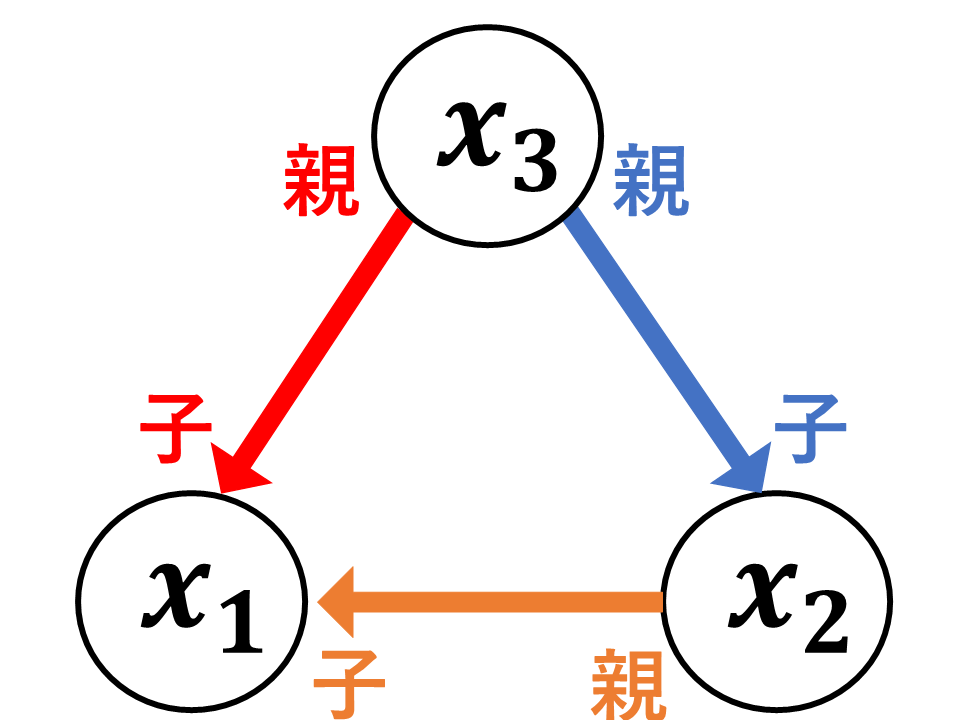
ベイジアンネットワークは図2のように, 親から子への矢印により条件付き確率を表現することで変数間の因果関係を表現する.
図2. ベイジアンネットワーク
例えば, 図2の場合には以下の確率を表現している.
\begin{eqnarray}
p(x_{1}, x_{2}, x_{3}) = p(x_{1}|x_{2}, x_{3})p(x_{2}|x_{3})p(x_{3})
\end{eqnarray}
このように, ベイジアンネットワークはN個の確率変数$X = \{x_{1}, x_{2}, ... x_{N}\}$に対して条件付き独立を考慮することで, 以下のような因数分解を行っている.
\begin{eqnarray}
\label{bayes}
p(X) = \prod_{n=1}^{N}p(x_{n}|x_{\text{pa}(n)})
\end{eqnarray}
ここで, $\text{pa}(n)$は$x_{n}$の親ノードの集合とする. 一般的に, $N$個の変数の確率を求めるには$O(K^{N})$の計算量を必要とするが, このように条件付き独立を考慮することで, $O(NK)$での計算を可能とする.
2. マルコフ確率場(無向グラフ)
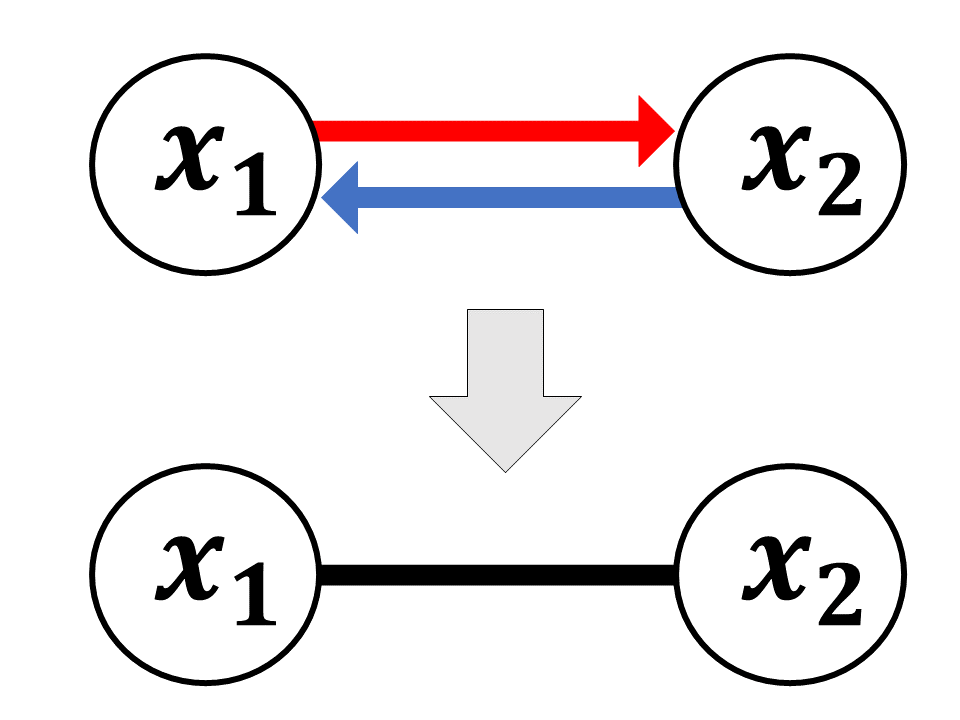
変数間に双方向の因果関係が存在するとき, ベイジアンネットワークでは図3のように両方の向きに矢印を引く必要がある. このような場合, 確率変数間に無向リンクをはることで, モデルを捉えやすくなる.
図3. 双方向の因果関係
マルコフ確率場における因数分解では, ポテンシャル関数$\phi$を用いて, $N$個の確率変数$X$を$C$個の部分集合$X_{c} \subseteq \{x_{1}, ..., x_{N}\} (c=1, ..., C)$に分解する.
\begin{eqnarray}
\label{markov}
p(X) = \frac{1}{Z}\prod_{c=1}^{C}\phi_{c}(X_{c})
\end{eqnarray}
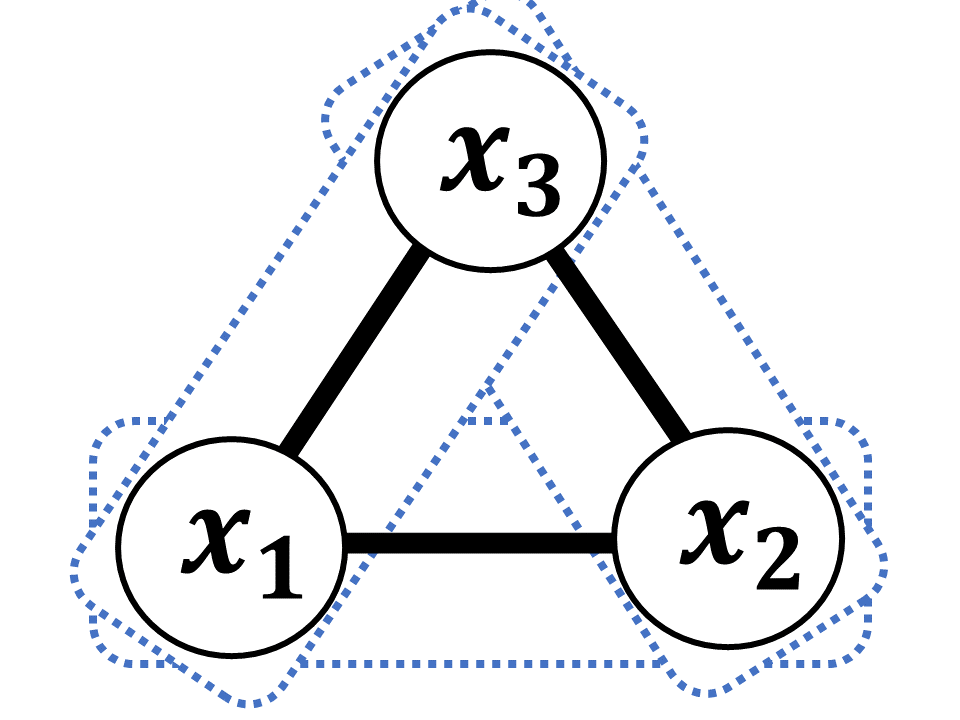
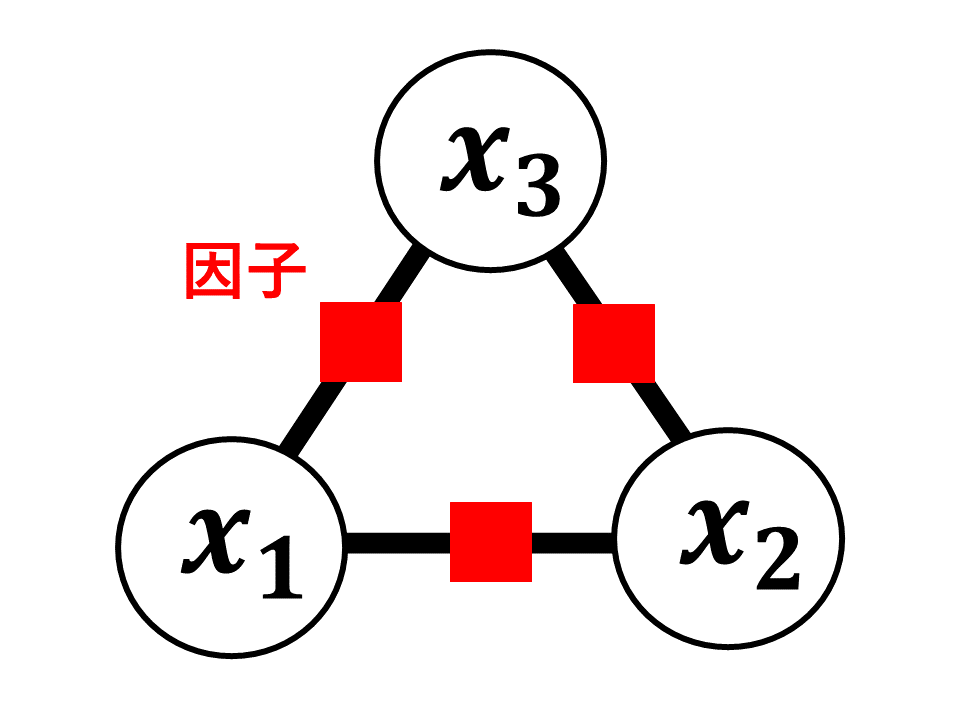
ここで, $Z$は規格化定数であり, ポテンシャル関数$\phi$が確率分布でない場合にも全体の総和が1となるような正規化項としてはたらく. また, グラフの部分集合$X_{c}$をクリークとよび, 1つのグラフにはさまざまなクリークの捉え方がある. 例えば, 図4のようにクリークを形成したとする.
図4. クリークの例
この場合, 同時分布は以下のように因数分解できる.
\begin{eqnarray}
\label{markov_bunkai}
p(x_{1}, x_{2}, x_{3}) = \phi_{1}(x_{1}, x_{2})\phi_{2}(x_{2}, x_{3})\phi_{3}(x_{3}, x_{1})
\end{eqnarray}
3. 因子グラフ
因子グラフは超グラフを用いることで, 図5のように, マルコフ確率場におけるクリークを直接的に表現する.
図4. 因子グラフ
超グラフは, 1つの辺が2つの頂点から成り立つ通常のグラフとは異なり, 1つの辺が複数の頂点を結ぶ(超辺と呼ぶ). この超辺を因子とし, 以下の式によってグラフを表現できる.
\begin{eqnarray}
\label{Inshi}
p(X) = \frac{1}{Z}\prod_{a=1}^{A}\Psi_{a}(X_{a})
\end{eqnarray}
ここで, $Z$は規格化定数であり, $\Psi_{a}$は因子関数と呼ばれる. また, $Z$は以下の式で表される.
\begin{eqnarray}
\label{Inshi_bunkai}
Z = \sum_{x_{a}}\prod_{a=1}^{A}\Psi_{a}(X_{a})
\end{eqnarray}
また, 規格化定数$Z$を正確に計算することは一般(計算量的)に困難であるため, 頂点$i$に対する近傍の条件付き確率で近似をすることが多い.
4. 条件付き確率場
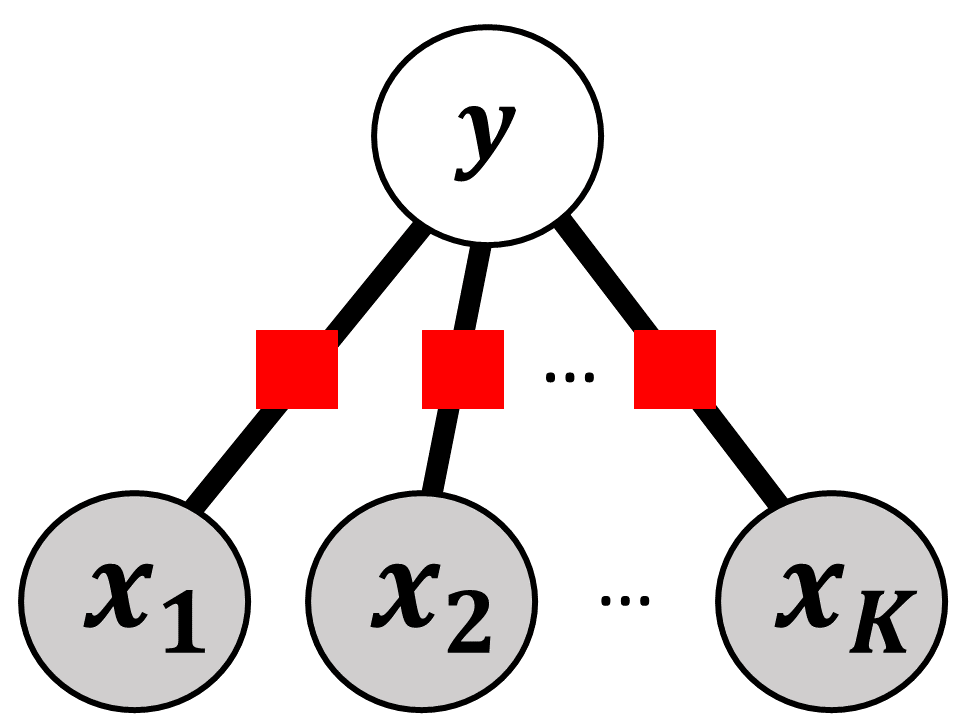
条件付き確率場は, 図5のロジスティック回帰を多クラスに拡張したものであり, 系列データにおける識別問題を表現することができる.
図5. ロジスティック回帰モデル
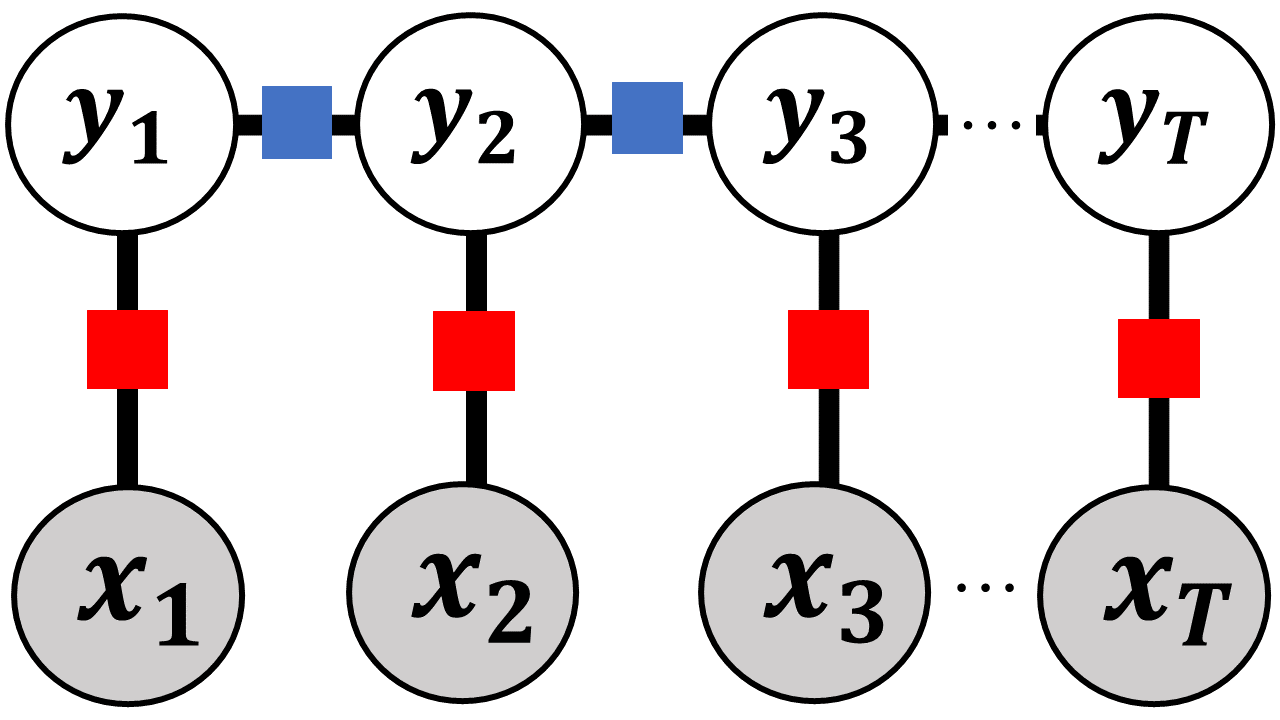
T時刻の入力変数$X = \{x_{1}, x_{2}, ..., x_{T}\}$に対して, 各時刻の変数$Y = \{y_{1}, y_{2}, ..., y_{T}\}$を推定する場合, 条件付き確率場のグラフは図6のように表される.
図6. 線形条件付き確率場
このとき, 図6は以下の式で表現できる.
\begin{eqnarray}
p(Y|X) = \frac{1}{Z(X)}\prod_{t=1}^{T}\text{exp}\{\sum_{n=1}^{N}\theta_{n}f_{n}(Y_{t}, Y_{t-1}, X_{t})\}
\end{eqnarray}
ここで, 各時刻の確率は独立であると仮定し, $t$時刻の推定結果$y_{t}$に影響を与えるのは, 1時刻前の推定結果$y_{t-1}$とその時刻の入力$x_{t}$のみと仮定する. この仮定により作られる識別器を線形条件付き確率場と呼び, 最もよく用いられる条件付き確率場となる.
隠れマルコフモデル(HMM)が有向グラフで表される系列データの識別機であるのに対し, 線形条件付き確率場(Linear CRF)は, HMMの無向グラフバージョンと言える.
参考資料
cf) グラフィカルモデル (機械学習プロフェッショナルシリーズ)
cf) PROBABILISTIC GRAPHICAL MODELS
cf) An Introduction to Conditional Random Field
